Раздел 6. Задачи скалярной оптимизации, линейные, нелинейные, дискретные

6.7 Задача распределения ресурсов

Это едва ли не самая распространённая операция. Под ресурсом в общем случае понимают физическую или абстрактную величину, которую система использует для производства полезного продукта. Например: горючее, деньги, время, объём склада. Как правило – ресурс ограничен, поэтому встаёт задача как распределить ресурс между отдельными элементами системы, чтобы суммарный эффект был максимальным.

Рассмотрим классическую задачу распределения ресурсов.

Имеется начальное количество ресурсов k₀ , которые необходимо распределить между двумя отраслями. Каждая отрасль работает в течении m лет. Если в первую отрасль в i - ый год вкладываются средства X _i, то доход 𝒇(X _i), если же во вторую вкладываются Y_i, тогда доход 𝓰(Yi ). Средства тратятся, принося доход, а новых средств не поступает и полученный доход не вкладывается.

Нас интересует суммарный доход: .Суммарный выигрыш равен сумме выигрышей на каждом шаге. Состоянием системы является количество средств перед i - ым шагом. Так как новых средств не поступает, то ресурсы уменьшаются.

Управление Y_i может быть записано как Y_i = k - X_i. После i - го шага в первой отрасли остаются средства 𝜑(X_i), а во второй 𝜓(Y_i) = 𝜓(k - X _i). Эти функции называются функциями траты. Мы можем составить уравнение Беллмана. В этой задаче на i-ом шаге одно управление X_i и одно состояние k

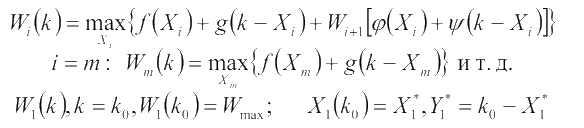
Исследуя функции траты, получим количество средств после i - го шага: 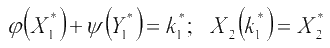и т.д.

Задача о распределении ресурсов допускает геометрическую интерпретацию. X₁ + Y₁ = k₀

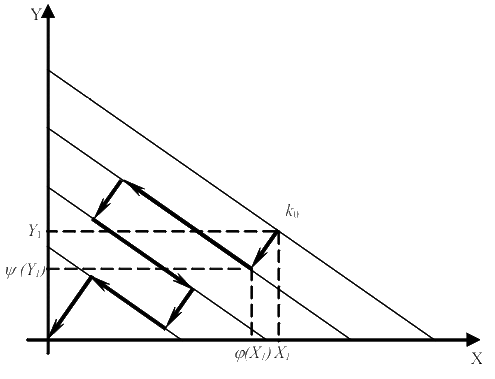
Распределение на первом шаге – указание точки на гипотенузе. После этого средства тратятся. Распределение средств – движение внутрь треугольника. Рассмотрим частные случаи задач о распределении ресурсов.

Распределение по неоднородным этапам.

Выше мы считали, что все функции одинаковы на всех этапах. Во многих задачах функции меняются от этапа к этапу: 𝒇_i(X_i), 𝓰_i(Y_i); 𝜑_i(X_i),𝜓_i(Y_i). Покажем, что процедура динамического программирования принципиально не меняется. Запишем уравнение Беллмана:

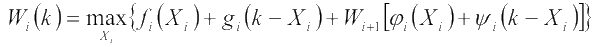
Распределение ресурсов между тремя и более отраслями.

В этом случае на каждом шаге будет уже n управлений, но одно из них может быть выражено как: 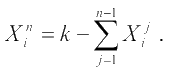В этом случае, в правой части уравнения Беллмана будет две и более переменных, по которым ищется максимум, и задача усложняется.

Распределение ресурсов с резервированием.

В такой модели если средства распределяются между двумя отраслями, то какое-то количество средств можно оставить до последующего распределения. В этом случае задача имеет смысл даже для одной отрасли. Начальное количество средств разделяется на первом этапе на X 1 и на k - X1 (резерв), на втором этапе подлежат разделению средства из резерва. Такую задачу можно представить как с одной отраслью реальной, а другой фиктивной (не приносящей доход и не расходующей средства). Решение такой задачи сводится к классической, задав функции дохода и трат.

𝒇(X), 𝓰(Y) = 0 - функции дохода; 𝜑(X) = 𝜓(Y) - функции трат

Подставив их в уравнение Беллмана, можно решить задачу как классическую. Задача может быть упрощена до следующей:

Пусть вид функции f (X i ) не убывающий в этом случае недоиспользовать средства не выгодно. В этом случае решение допускают теоремы, обосновывающие, если:

1. f(X) неубывающая и выпуклая вверх, оптимальное распределение ресурсов равномерное
2. f(X) возрастающая и выпуклая вниз, оптимальное решение – вложить все средства в один этап, и ничего не зарезервировать.

Таким образом, приходим к классической задаче.

Задача с резервированием в одной отрасли при параллельных функциях траты. Все функции траты 𝜑(x_i) = 0 .

В этом случае задача сводится к более простой.

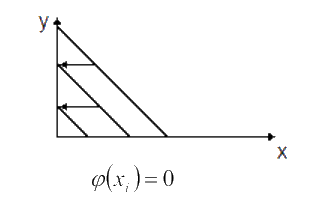
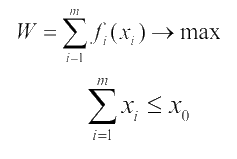
Рассмотрим более частный случай: все функции одинаковые на всех шагах.

𝒇_i(x) = 𝒇(x), ∀_i

эти функции не убывающие.

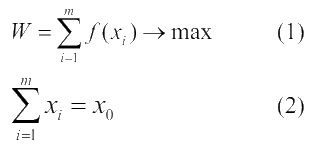
(2) – равенство, т.к. функция неубывающая и недоиспользование средств невыгодно. Это имеет теоретическое обоснование:

1. если функция неубывающая и выпуклая вверх, то оптимальным распределением является равномерное распределение.
2. Если функция неубывающая и выпуклая вниз, то оптимальным распределением является такое: все распределение в один этап (элемент) и ничего в другие.

Распределение ресурсов «с вложением доходов в производство».

В классической задаче считается, что полученный доход на i - ом шаге в производство не вкладывается, т. е. он отчисляется и подсчитывается как эффект. Во многих задачах полученный эффект можно использовать как ресурс для следующего шага объединяя его с оставшимся ресурсом. Если ре- сурс не деньги, то средства можно привести к единому эквиваленту с оставшимися средствами. Такая модель является развитием классической модели. Так как оставшиеся средства и доход объединяются, то можно ввести единую интегральную функцию – функцию изменения средств. F (X_i)- количество оставшихся средств плюс доход после i - го шага, если вложили X_i.

k - количество средств перед i - м шагом.

Выигрыш на i - ом шаге зависит от того, как мы подсчитываем доход (эффект) от управления всеми ресурсами. Поставим задачу: максимальный доход в конце m - го шага.

Тогда на всех шагах 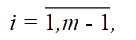доход = 0, W_i= 0 . На m - ом шаге выигрыш W_m = F_m(X_m) + G_m(k - X_m). Подставив эти выражения в уравнение Беллмана, мы программируем задачу от начала к концу, если имеется начальное количество средств k₀ . Здесь функция траты: k^' = F_i(X_i) + G_i(k - X_i).

Частный случай: когда F и G неубывающие. В этом случае чем больше значение доход + средства получается в конце i - го шага, тем лучшим условием это будет для проведения (i +1)- го шага. Поэтому можно не заботиться о следующих шагах, достаточно обеспечить максимум на каждом шаге.

Таким образом процедура оптимизации возможна в одном направлении от начала к концу, т. е. задача динамического программирования вырождается в задачу последовательной оптимизации.

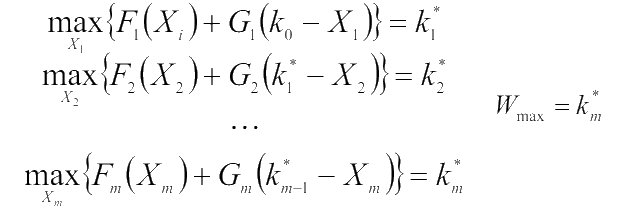
Рассмотрим задачу распределения ресурсов с вложением доходов в производство и отчислением. Это наиболее общий случай. Разделим функции дохода и функции траты: 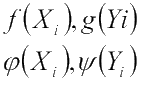и максимальный суммарный отчисленный доход + оставшиеся средства после m - го шага. Введём функцию отчисления r_i(D_i); D - доход. Тогда выигрыш на каждом шаге:

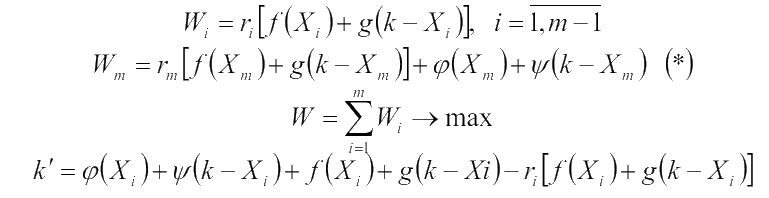
Уравнение Беллмана для i - го шага будет выглядеть так:

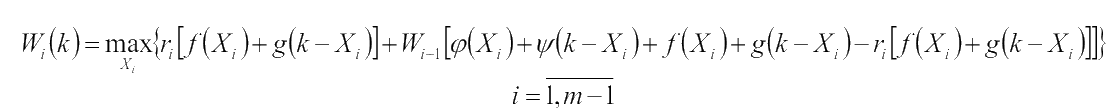
для i = m надо учесть (*).

Если r_i = 1 , то мы получаем классическую задачу.

Учёт предыстории процесса.

Мы считаем, что функции как выигрыша, так и траты зависят от состояния перед i - ым шагом, т. е. не зависят от более ранних состояний. Такие процессы называются процессами без памяти. Но иногда при рассмотрении процессов, связанных с «живыми» организациями требуется помнить всю историю происходящего. Такая задача более сложна. Введём расширенное состояние:

S = (S,S_i-1, S_i-2,...,S_i-L)

S_i-L − состояние за L шагов до i − го. Тогда W_i (S,U_i ), 𝜑(S,U_i ),. Но задача сложна вычислительном аспекте. Пусть S имеет k координат и предыстория распространяется на L шагов, тогда результат k × L . Вот почему подобные задачи можно решать если k × L ≤ 3 .

Задача с мультипликативным критерием.

До сих пор мы считали, что суммарный выигрыш равен сумме выигрыш на i - ом шаге. Но есть задачи, где общий критерий равен произведению критериальных величин на каждом шаге. В этом случае так же можно применить уравнение Беллмана.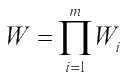, но вместо этого можно взять функцию W^' = lnW . Оптимальные решения будут одинаковы ввиду многоэтапности функций. Но можно при вводе уравнения Беллмана учесть, что: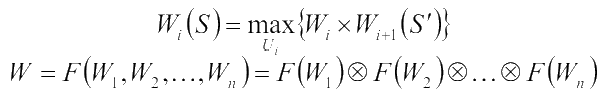

Пример: устройство состоит из n узлов. Имеется некоторое устройство k₀ , которое может использоваться для повышения надёжности каждого узла. Необходимо так распределить ресурс, чтобы суммарная надёжность была максимальной.

q(X_i) - надёжность каждого узла.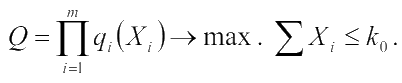

Операции не связанные со временем.

Во многих задачах распределение ресурсов не связано с временными шагами. Ресурс обычно распределяется по объектам. Например, если расписать распределение ресурсов между n объектами и на каждый объект задана функция выигрыша, то такая задача эквивалентна рассмотренной нами задаче о распределении ресурсов с резервированием в одной отрасли по n шагам.

---

Предыдущая лекция  |  Следующая лекция