Раздел 7. Многокритериальные задачи, парето-оптимальность, схемы компромиссов
7.4 Парето-оптимальность
Многокритериальная задача оптимизации вместе со множеством возможных (допустимых) решений Ω включает набор целевых функций J1,J2,...,Js (векторный критерий), обозначаемый
J̅ (x̅ ) = (J1 (x̅ ), J2 (x̅ ),...,Js (x̅ )).
Аналогично со множеством допустимых решений Ω, пусть множество Λ — область критериев
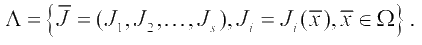
Каждому решению x̅ ∈ Ω соответствует один вполне определенный векторный критерий J̅ (x̅ ). С другой стороны, каждой оценке J̅i (x̅ ) могут отвечать несколько решений x̅ ∈ Ω . Таким образом, между множествами Ω и Λ имеется тесная связь, и поэтому выбор решения из множества Ω в указанном смысле равносилен выбору соответствующей оценки из множества Λ. Таким образом, при существовании в задаче нескольких частных критериев можно рассматривать задачу многокритериальной оптимизации, как задачу нахождения такого вектора, который обеспечивает одновременно минимальное значение каждому частному критерию оптимальности:
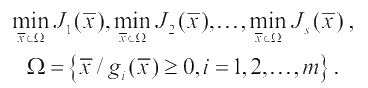
Любые два векторных критерия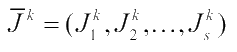 
и 
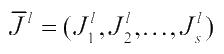являются
противоречивыми, если частные критерии находятся в соотношениях
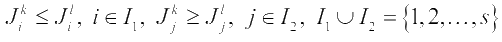
и по крайней мере одно из этих соотношений является строгим. В случае доминирования J̅ k над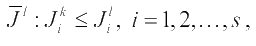 
и хотя бы для одного i это неравенство строгое, альтернатива x̅ l может быть исключена из рассмотрения, так как вектор
J̅ k лучше вектора J̅ l по всем частным критериям. В этом случае при переходе от критерия
J̅ l к критерию J̅ k ни один из частных критериев не ухудшится, а хотя бы один из них будет улучшен.
Множество критериев, для которых всегда справедлив принцип доминирования, образует множество Λ s (Λ s ⊆ Λ) которое называется областью согласия. В области согласия нет противоречия между частными критериями оптимальности, и, если область критериев состоит только из области согласия, тогда существует единственная точка x̅ * ∈ Ω, в которой все частные критерии согласованы между собой в том смысле, что при движении к x̅ * значения всех компонент Ji (x̅ ) уменьшаются (увеличиваются). Точка x̅ * является оптимальным решением, и при этом значения всех частных критериев достигают в ней минимума (максимума).
Такая ситуация на практике встречается крайне редко, наиболее типичным является случай, когда частные критерии являются противоречивыми и минимум по каждому из них достигается в различных точках. В этом случае уменьшение одного частного критерия приводит к увеличению других частных критериев. Такие точки x̅ 0 ∈ Ω , в которых не выполняется принцип доминирования относительно любой точки x̅ ∈ Ω , являются эффективными точками, то есть точка x̅ 0 ∈ Ω называется эффективной, если не существует ни одной точки x̅ ∈ Ω такой, что Ji (x̅ ) ≤ Ji (x̅ 0 ), i = 1,2,...,s и хотя бы для одного i это неравенство строгое, т. е. Ji (x̅ ) < Ji (x̅ 0 ). Поскольку в эффективных точках критерий J̅ является не уменьшаемым по всем частным критериям одновременно, то эти точки также называются неулучшаемыми решениями или оптимальными по Парето. Примером множества неулучшаемых решений в двумерном случае может служить кривая между точками C и D (рис. 1).
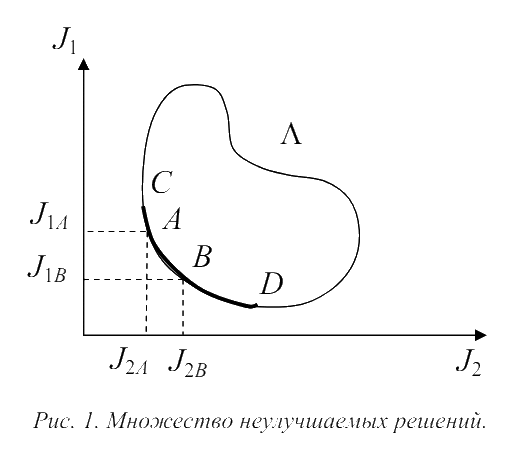
Точки А и В являются безусловными точками неулучшаемых решений, поскольку любое улучшение для одной цели J1 вызывает ухудшение для другой выбранной цели J2 , т. е. J1B < J1A, J2B > J2A. Таким образом, при многокритериальной оптимизации необходимо ограничиться множеством точек неулучшаемых решений, а сама оптимизация должна включать в себя определенную генерацию и выбор точек с неулучшаемыми решениями.
Множество векторных критериев, соответствующих множеству всех эффективных точек, называется областью компромиссов Λ k (Λ k ⊂ Λ), а само множество эффективных точек — областью решений, оптимальных по Парето. Оптимальность по Парето означает, что нельзя дальше уменьшать значение одного из частных критериев, не увеличивая при этом хотя бы одного из остальных, таким образом, в области компромиссов Λ k не выполняется принцип доминирования, а частные критерии являются противоречивыми. Это приводит к необходимости введения компромисса между частными критериями оптимальности для того, чтобы решить, какой из векторов J̅ l или J̅ k из области компромиссов Λ k k считать предпочтительным. Оптимально-компромиссным решением является одна из эффективных точек x̅ 0 ∈ Dx , являющаяся предпочтительней с точки зрения проектировщика. Таким образом, задача векторной оптимизации не позволяет однозначно ответить на вопрос, получено ли оптимальное решение. Положительный ответ на этот вопрос зависит от качественной информации о важности частных критериев.
В соответствии с принципом Парето, решение должно принадлежать множеству Парето, а искать это решение необходимо на границе множества.