Раздел 9. Принятие решений в условиях неопределенности

9.1 Игровые модели принятия решений

Игровая модель представляет собой особый вид модели ТПР . Встречается довольно много ситуаций в экономике, особенно в военных операциях, где действует несколько сторон, преследующих различные интересы. И поэтому, невозможно оценить результат принимаемого решения единообразно. Такого рода ситуации называются конфликтными. Теория, описывающая конфликтные ситуации с количественной стороны, называется теорией игр. Интересы между сторонами могут быть полностью противоположными (антагонистические игры). Во многих ситуациях в игре могут принимать участие три и более сторон (множественные игры). Некоторые стороны могут объединяться по интересам(коалиционные).

Игра – модель ситуации, некоторая упрощенная схема, где зафиксированы сами игроки, правила игры, определѐнные выигрыши после каждого хода, правила окончания игры.

Допустимые действия каждого из игроков, направленные на достижение некоторой цели, называются правилами игры.

Количественная оценка результатов игры называется платежом.

Игра называется парной, если в ней участвуют только две стороны (два лица).

Парная игра называется игрой с нулевой суммой, если сумма платежей равна нулю, т.е. если проигрыш одного игрока равен выигрышу второго.

Ходы в игре могут быть личные и случайные. Личный ход зависит от сознательного решения стороны, а случайный ход – результат случайного механизма, который иногда применяется специально.

Однозначное описание выбора игрока в каждой из возможных ситуаций, при которой он должен сделать личный ход, называется стратегией игрока.

Если количество стратегий конечно – игра конечная, в противном случае – бесконечная игра.

Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает игроку максимально возможный средний выигрыш (или, что то же самое, минимально возможный средний проигрыш).

Задачей теории игр является обоснование оптимальных стратегий обоих игроков. В теории игр считается, что игра повторяется многократно и игроков интересует средний выигрыш.

Платёжная матрица

Рассмотрим конечную игру, в которой игрок А ("мы") имеет т стратегий, а игрок В ("противник") — n стратегий. Такая игра называется игрой m × n. Будем обозначать наши стратегии А₁, А₂, ..., А_m; стратегии противника — В₁, B₂, ..., B_n. Предположим, что нам известны значения а_ij при каждой паре стратегий.Эти значения можно записать в виде прямоугольной таблицы (матрицы), строки которой соответствуют нашим стратегиям (A_i), а столбцы — стратегиям противника (В_j).Такая таблица называется платежной матрицей или просто матрицей игры. Если есть случайные ходы, то выигрыш так же случаен, и можно взять математическое ожидание выигрыша. Построить матрицу можно не всегда из-за еѐ большого размера (например, игра в шахматы). Для игр с полной информацией, т. е. когда один игрок знает, как поступил второй, всегда можно построить платѐжную матрицу.

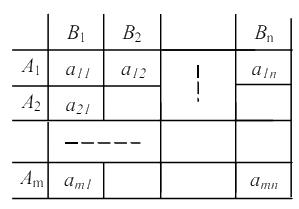
Верхняя и нижняя цены игры

Величина 𝛼 = i^max j^{min a_ij} называется нижней ценой игры или максимином. Величина 𝛽 = j^max i^{min a_ij} называется верхней ценой игры или минимаксом. Итак, мы можем сразу найти 𝛼 и 𝛽 анализируя матрицу.

Игра, для которой 𝛼 = 𝛽, называется игрой с седловой точкой

Рассмотрим простейшие примеры игр:

1) Игра поиск. Игрок A прячется в первом или втором месте. Игрок B ищет его. Если игрок B находит A, то A платит ему один рубль, если же B не находит A, то B платит один рубль A. Построим платежную матрицу.

Решение этой игры: 𝛼 = -1, 𝛽 =1.

2) Игра три пальца. игроки A и B одновременно показывают один, два или три пальца. Выигрыш равен сумме, причем если получилось четное число очков, выигрывает A, а если нечeтное, то B. Строим платежную матрицу.

Решение у этой игры: 𝛼 = -3, 𝛽 = 4 .

3) Игра вооружение – самолѐты. У стороны A есть три вида вооружения: зенитка, ракета и автомат. У B – три типа средств нападения. Известны вероятности, с которыми каждый i -ый тип вооружения A сбивает каждое j -ое средство противника B. Построим платѐжную матрицу. Решение для этой игры: 𝛼 = 𝛽 = 0,7 . Такое решение называется седловой точкой.

Принцип чистых стратегий

Если игра имеет седловую точку, то говорят, что игра решается в чистых стратегиях. Такое решение обладает свойством устойчивости, т. е. если один игрок придерживается своей оптимальной стратегии, то другому игроку невыгодно отклоняться от своей оптимальной стратегии. Это свойство устойчивости полагается в основу понятия оптимальной игры. В игре может быть несколько седловых точек, но, как правило, таких точек нет, и нельзя найти решение в чистых стратегиях. Если игра, заданная матрицей, не имеет седловой точки, то для нахождения ее решения используются смешанные стратегии.

Смешанные стратегии

Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называется смешанной стратегией данного игрока. Сумма компонент указанного вектора равна единице, а сами компоненты не отрицательны.

Обычно смешанную стратегию первого игрока обозначают как вектор p = (p₁, p₂, ..., p_m), а второго - q = (q₁, q₂, ..., q_n ), где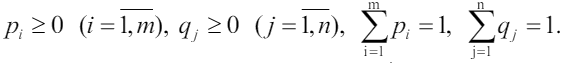

Если p* – оптимальная стратегия первого игрока, а q* – оптимальная стратегия второго игрока, то число 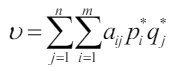является ценой игры.

С применением смешанных стратегий всегда можно найти решение, обладающее устойчивостью. Решением игры называется пара оптимальных смешанных стратегий (S^*_A S^*_B) обладающих следующим свойством: если один из игроков придерживается своей оптимальной смешанной стратегии, то другому не может быть выгодно отступать от своей. Выигрыш соответствующего оптимального решения называется ценой игры.

Основная теорема теории игр

Каждая конечная игра имеет по крайней мере одно решение, возможно в области смешанных стратегий. Цена игры заключена в пределах 𝛼 ≤ J ≤ 𝛽. Введем понятие активной стратегии – стратегии, которая входит в решение с вероятностью большей нуля.

Теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равен цене игры J независимо от того, что делает другой игрок, если только тот не выходит за пределы своих активных стратегий.

Доказательство: пусть получена оптимальная стратегия S игрока A:

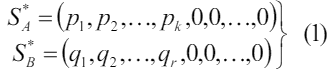
Применение решения (1) дает выигрыш J. Пусть B пользуется чистыми стратегиями, в результате получим выигрыш J₁.

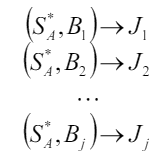
По определению решения игры следует, что отклонение от своей стратегии невыгодно для игрока: J₁ ≥ J, J₂ ≥ J,...,J_j ≥ J,...,J_n ≥ J. Посмотрим, может ли быть J_j ≥ J, т. е. существует ли такое J. Выразим цены игры, полученные при применении смешанной стратегии как величину математического ожидания: M (J) = J₁q₁ + J₂ q₂ + ... + J_rq_r.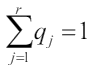. Получается, что чистая цена игры – это математическое ожидание, если какая-то случайная величина J_l > J,а все остальные равны J, то среднее значение должно быть больше J, , а не равно ему, так как ни одна случайная величина не может быть больше МО.

Упрощение игр

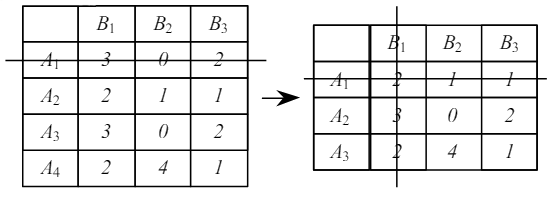
Если в игре построена платежная матрица, то игру возможно упростить, т. е. заранее отбросить такие стратегии игроков, которые не могут быть выгодными ни при каких обстоятельствах. Итак, вычеркиваем заведомо невыгодные и дублирующие стратегии: дублирующая стратегия – это строка A1. Стратегия A2 заведомо невыгодна, а при просмотре столбцов – невыгодны большие векторы, поэтому B1 так же вычеркиваем.

Таким образом, если записана платѐжная матрица, можно ее упростить, вычислить 𝛼 и 𝛽, и если они не равны друг другу, принимаются за решение смешанной стратегии.

Решение игр 2 × 2

Если в такой игре нет седловой точки, то все стратегии являются активными. Если же седловая точка есть, то игра может быть решена путѐм отбрасывания заведомо невыгодных решений. Все стратегии активные, значит можно применить теорему об активных стратегиях:

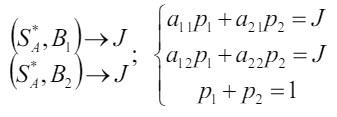
Решая эту систему получим:

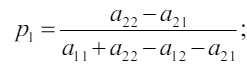
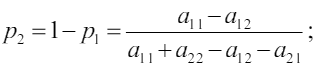
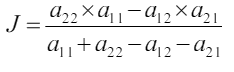
Для игрока B:

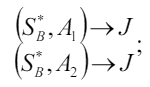
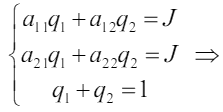
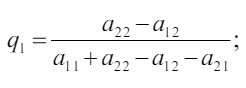
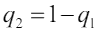
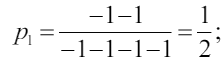
Пример: игра в «прятки»:

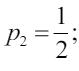
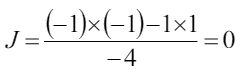
Геометрическое решение игр 2 × 2.

Игры с двумя стратегиями можно решить геометрически. Для этого начинаем решать игру со стороны игрока, у которого две стратегии.

Пусть этот игрок А.

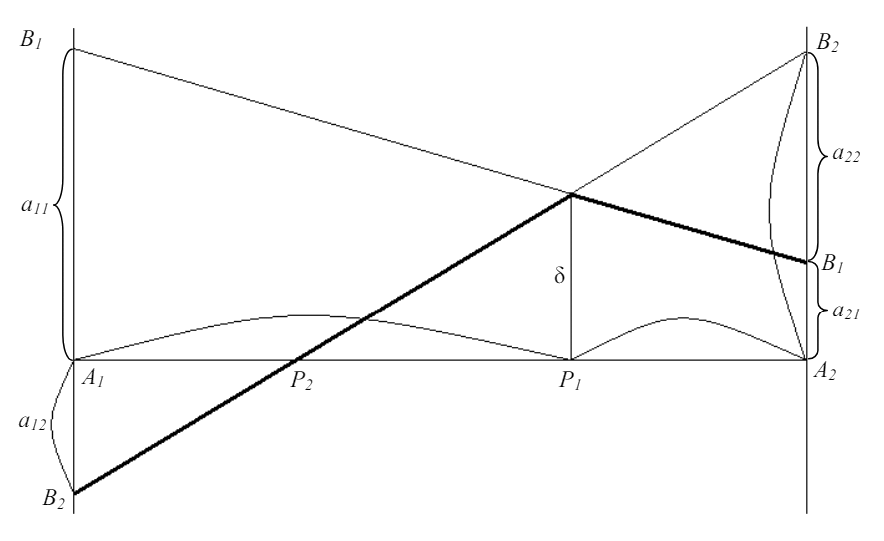
Решается по принципу минимакса для игрока А. Решение необязательно находится на пересечении линий.

Рассмотрим задачу со стороны игрока В.

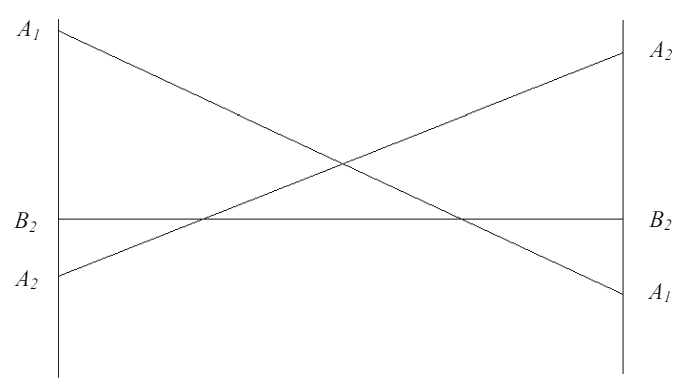
Если у одного игрока 2 стороны, а у другого много, то игру также можно решить геометрически.

В результате упрощения, игра имеет вид:

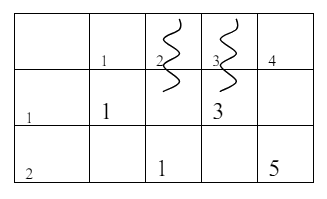
Решим игру относительно игрока А:

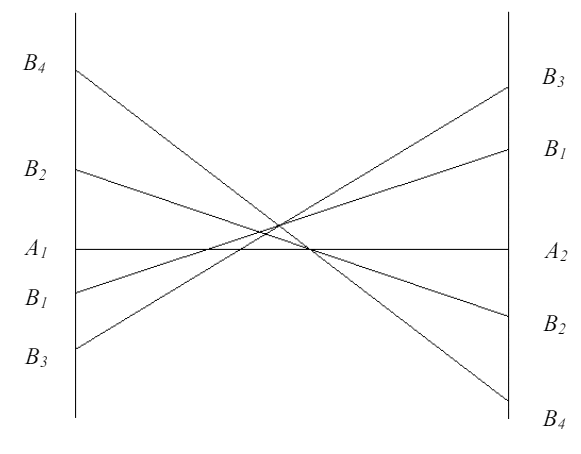
Для решения необходимо решить совместное уравнение В₄, В₁

Тангенс угла наклона

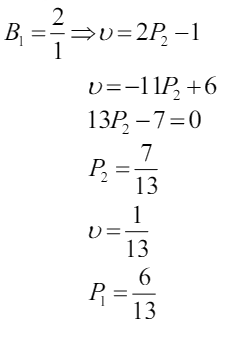
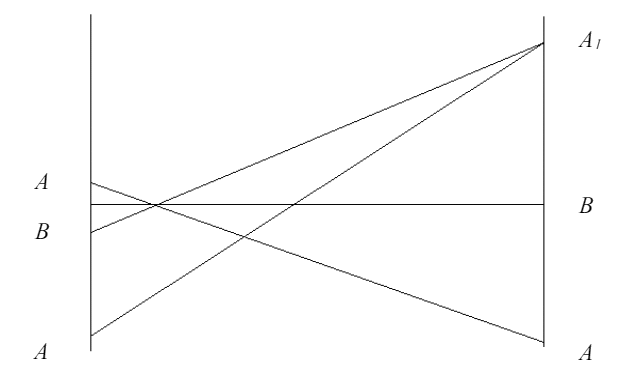
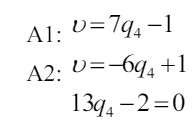
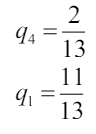
Решение игр m × n

Пусть у игрока A, m стратегий, а у B - n. В общем случае игра имеет решение в области смешанных стратегий. Таким образом, чтобы решить игру надо найти S^*_A и S^*_B . Пусть игрок A применяет свою оптимальную смешанную стратегию, а игрок B - чистую. При этом поучится выигрыш:

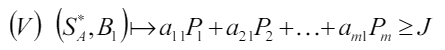
По определению решения игры, отклонение игрока B от своей оптимальной стратегии невыгодно для него. Если бы все стратегии были активными, то можно было бы поставить "=" в выражение (V).

В дальнейшем будем считать, что величина цены игры J > 0. Этого можно добиться, если первоначальную платежную матрицу a_ij сместить вверх, т. е. прибавить величину a₀ к каждому элементу матрицы. При этом решение игры не меняется.

Разделим левую и правую часть неравенств на величину J, и обозначим величины 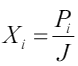. Тогда получим систему ограничений в следующем виде:

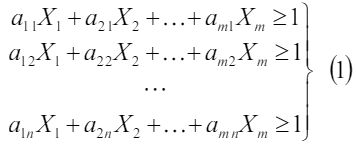
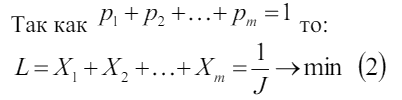
Так как необходимо выбрать такие вероятности p_i , что бы цена игры была максимальной, то можно считать, что L → min . Получили следующую задачу линейного программирования: найти такие неотрицательные величины X₁,X₂,...,X_m которые бы удовлетворяли системе уравнений (1)и при этом минимизировали линейную систему (2). Аналогично рассмотрим игру со стороны игрока B.

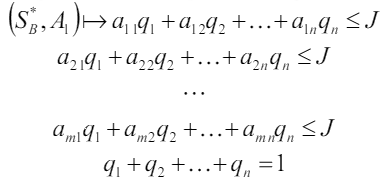
Аналогично делим на J и обозначим 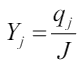. Получим задачу:

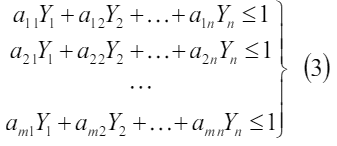
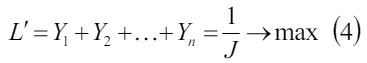
Так как игрок B стремится уменьшить выигрыш, то решение игры m × n может быть сведено к решению пары задач линейного программирования.

Рассмотрим вопрос существования решения задач (1), (2), (3), (4). Доказательство существования этого решения будет доказательством основной теоремы теории игр.

Доказательство: из теории линейного программирования известно, что задача линейного программирования не имеет решения в двух случаях:

1) Нет допустимого решения, т. е. система ограничений несовместна.

2) Целевая функция не ограничена.

Покажем, что любая пара задач линейного программирования имеет решение: возьмeм (1) и (2). Рассмотрим самый маленький выигрыш матрицы .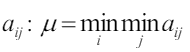

Тогда в качестве решения можно взять следующее: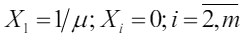 . Подставим это решение во все строки линейных неравенств (1). Так как 𝜇 - min, то, например, a₁₁/𝜇 > 1 всегда, а остальные равны нулю, то у нас есть решение всегда. Так как вероятности и цена игры больше нуля, поэтому X_i > 0. Так как L → min , то минимальная величина ограничена по крайней мере нулѐм, таким образом мы доказали, что решение (1) и (2) всегда существуют. А если существует (2), то существует J, и значит существует L_max во второй задаче. Мы доказали основную теорему теории игр: любая матричная игра имеет решение в области смешанных стратегий.

---

Предыдущая лекция  |  Следующая лекция